Research

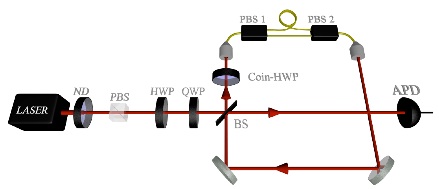
When one wants to be as certain as possible that an obtained measurement result is correct, one should use a maximum confidence quantum measurement strategy. This is a generalisation of unambiguous measurement strategies, to the case of distinguishing between linearly dependent quantum states. This work was done with Sarah Croke, Stephen Barnett, Claire Gilson and John Jeffers (PRL 96, 070401 (2006)). The figure to the right shows the experimental setup for a maximum confidence measurement to distinguish between three lifted trine states (PRL ).

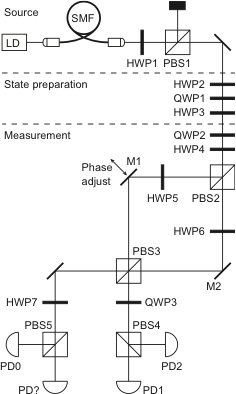
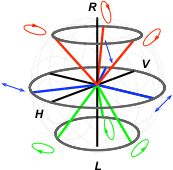
In the figure above, the Bloch vectors of the quantum states to be distinguished are shown in red, and the Bloch vectors corresponding to the maximum confidence measurement and the minimum uncertainty measurement are shown in green and blue, respectively.

Maximum confidence quantum measurements

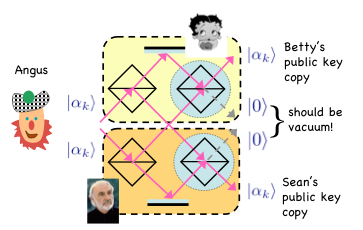
Quantum digital signatures

A digital signature scheme allows one party to securely sign a message so that recipients can be sure of its authenticity. The figure shows a setup for quantum digital signatures using coherent states. The experiment will be realised in collaboration with Prof Gerald Buller at Heriot-Watt University. It is based on work on quantum comparison of coherent states, done together with Igor Jex and Marcos Curty (PRA 74, 022304 (2006)).

Open quantum systems

An open quantum system is a quantum system whose dynamics is determined both by interactions internal to the system, and by influences from an environment. Markovian or memory-less behaviour of such a system is well understood. In this case, the master equation describing the time evolution of the open quantum system takes the familiar Lindblad form. Much less is known about the general character of non-Markovian master equations. Non-Markovian behaviour is frequently encountered in real physical situations. An example is a damped driven two-level atom. This is also a research area that is becoming of increasing importance with the realisation that error correction in quantum computing may not be adequately handled using Markovian master equations. Michael Hall, Jim Cresser and Erika presented a method of finding the Kraus representation corresponding to a given master equation and vice versa (J. Mod Opt. 54, 1695 (2007); special issue for QEP-17, Manchester, UK, 2006). More recent work together with S. Stenholm, Variational properties of a pumped dynamical system (accepted for publication in PRA).


Joint measurements of non-commuting observables

The expectation values of two or more non-commuting observables of a quantum system cannot all have precise values. For example, the intrinsic uncertainties in position and momentum of a quantum system must obey an uncertainty relation. If we are making a joint measurement of two or more non-commuting observables, meaning that we are measuring all the observables on the same quantum system, then the uncertainties in our measurement results must be even greater. One can derive the bound on a joint measurement of spin-1/2 observables from the no-signalling principle (PRA 72, 042104 (2005)), with Alain Aspect and Stephen Barnett). There are interesting connections between the bounds on joint measurements and Bell inequalities (PRA 72, 052116 (2005)), with Wonmin Son, Stephen Barnett and Myungshik Kim).


One way to accomplish a joint measurement of two or more observables would be to clone the quantum system to be measured, and then measure one observable on each cloned copy. Thomas Brougham (now a postdoc in Prague) and Erika derived the optimal cloner for a joint measurement of two spin-1/2 observables (PRA 73, 062319 (2006)).


We also looked at what measurement strategy is better if we have a finite number of identically prepared quantum systems available for measurement, and want to determine the expectation values of two or three non-commuting spin-1/2 observables (Phys. Rev. A 76, 052313 (2007)). We have also investigated entropic uncertainties for spin-1/2 observables.

Below are some examples of research topics.


Photons walking the line

We present the first robust implementation of a coined quantum walk over five steps using only passive optical elements. By employing a fiber network loop we keep the amount of required resources constant as the walker's position Hilbert space is increased. We observed a non-Gaussian distribution of the walker's final position, thus characterizing a faster spread of the photon wave-packet in comparison to the classical random walk. The walk is realized for many different coin settings and initial states, which opens the way for the implementation of a quantum walk-based search algorithm.

This is a collaboration between researchers at Heriot-Watt University, Czech Technical University in Prague, Hungarian Academy of Sciences, and the University of Erlangen. The experimental work was done at University of Erlangen in the group of Christine Silberhorn. Journal reference Phys. Rev. Lett. 104, 050502 (2010).

Optimal quantum measurements

A quantum system is tiny, and will in general be disturbed by a measurement. This means that it is non-trivial to derive the optimal measurement for a particular task, such as identifying the state of a quantum system, or obtaining maximum information about what the state is. Distinguishing between mirror-symmetric states is an example (PRA 65, 052308 (2002), with Stephen Barnett, Claire Gilson and Kieran Hunter). One can sometimes use the no-signalling principle to easily derive optimal quantum measurements (PRA 65, 044307 (2002), with Stephen Barnett).


Together with Michael Hall and Thomas Brougham, we have looked at how to maximise the correlation between measurements made on the parts of a bipartite quantum system (PRA 74, 062308 (2006)).


Realising generalised quantum measurements

Once we know what the optimal quantum measurement is, we have to figure out how to realise it in an experiment. For photons, one can use an optical network. Using atoms or trapped ions, we could use Raman pulses to couple the internal levels, and then perform a fluorescence measurement to read out the measurement result (PRA 63, 052301 (2001), with Sonja Franke-Arnold, Stephen Barnett and Stig Stenholm). In an analogous way, generalised quantum measurements could be realised on atoms trapped in microstructures (PRA 64, 032303 (2001)).

Ancilla-driven universal quantum computation (ADQC) We propose a method of manipulating a quantum register remotely with the help of a single ancilla that steers the evolution of the register. The fully controlled ancilla qubit is coupled to the computational register solely via a fixed unitary two-qubit interaction, E, and then measured in suitable bases. We characterize all interactions E that induce a unitary, step-wise deterministic measurement back-action on the register sufficient to implement any arbitrary quantum channel. Our scheme offers significant experimental advantages for implementing computations, preparing states and performing generalized measurements as no direct control of the register is required. This work, arXiv:0911.3783v1, Phys. Rev. A 82, 020301 (2010) (R). and arXiv:0905.3354v2, is done in collaboration with Daniel Oi (Strathclyde), Elham Kashefi (Edinburgh University), and Janet Anders and Dan Browne (UCL). Binary search trees for generalized measurement Generalized quantum measurements (POVMs or POMs) are important for optimally extracting information for quantum communication and computation. The standard realization via the Neumark extension requires extensive resources in the form of operations in an extended Hilbert space. For an arbitrary measurement, we show how to construct a binary search tree with a depth logarithmic in the number of possible outcomes. This could be implemented experimentally by coupling the measured quantum system to a probe qubit which is measured, and then iterating. This is joint work with Daniel Oi at Strathclyde University (Phys. Rev. A 77, 052104 (2008)).http://arxiv.org/abs/0911.3783http://link.aps.org/doi/10.1103/PhysRevA.82.020301http://arxiv.org/abs/0905.3354http://link.aps.org/doi/10.1103/PhysRevA.77.052104http://link.aps.org/doi/10.1103/PhysRevA.77.052104http://link.aps.org/doi/10.1103/PhysRevA.82.020301shapeimage_6_link_0shapeimage_6_link_1shapeimage_6_link_2shapeimage_6_link_3shapeimage_6_link_4