I have moved to University of Edinburgh.

You should be automatically referred to my new website shortly.

Guided Ecological Simulation for Artistic Editing of Plant Distributions in Natural Scenes

Gwyneth A. Bradbury, Kartic Subr, Charalampos Koniaris, Kenny Mitchell, Tim Weyrich1

Journal of Computer Graphics Techniques (JCGT), 4(4), 28-53, November 2015. Invited for oral presentation at i3D 2016.

Author preprint (Low res. 1MB pdf)

Project page with hi-resolution images and slides

Video: Embedded below

Online View Sampling for Estimating Depth from Lightfields.

Changil Kim, Kartic Subr, Kenny Mitchell, Alexander-Sorkine Hornung, Markus Gross

International Conference on Image Processing, 2015.

Author preprint (3MB pdf)

Project page

Error analysis of estimators that use combinations of stochastic sampling strategies for dir. illum.

Kartic Subr, Derek Nowrouzezahrai, Wojciech Jarosz, Jan Kautz and Kenny Mitchell

Computer Graphics Forum (Proceedings of EGSR 2014), 33(4): 93-102, June 2014.

Author preprint (3MB pdf)

Derivations (Supplementary material A)

Slides: (3MB)

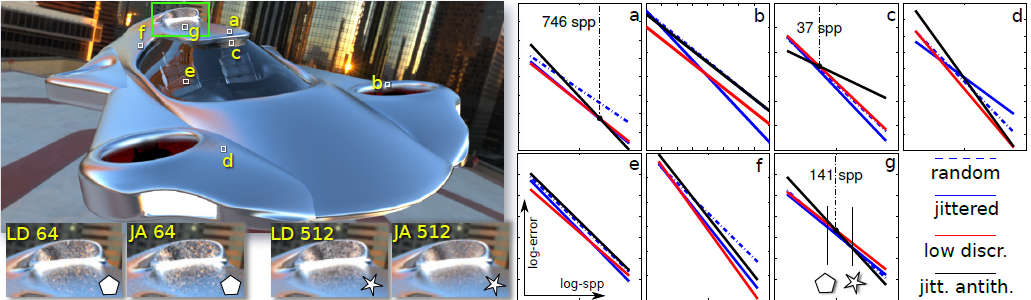
We present a theoretical analysis of error of combinations of Monte Carlo estimators used in image synthesis. Importance sampling and multiple importance sampling are popular variance-reduction strategies. Unfortunately, neither strategy improves the rate of convergence of Monte Carlo integration. Jittered sampling (a type of stratified sampling), on the other hand is known to improve the convergence rate. Most rendering software optimistically combine importance sampling with jittered sampling, hoping to achieve both. We derive the exact error of the combination of multiple importance sampling with jittered sampling. In addition, we demonstrate a further benefit of introducing negative correlations (antithetic sampling) between estimates to the convergence rate. As with importance sampling, antithetic sampling is known to reduce error for certain classes of integrands without affecting the convergence rate. In this paper, our analysis and experiments reveal that importance and antithetic sampling, if used judiciously and in conjunction with jittered sampling, may improve convergence rates. We show the impact of such combinations of strategies on the convergence rate of estimators for direct illumination.

Fourier Analysis of Stochastic Sampling Strategies for Assessing Bias and Variance in Integration

Kartic Subr and Jan Kautz

To appear, ACM Transaction on Graphics (Proceedings SIGGRAPH 2013) 32(4), July 2013

Erratum (publ. 2014)

Eq.5 should be an inequality --- inequality 16 (Sec.3) (Suppl. Mat. A of our EGSR14 paper).

Preprint (61MB pdf) (2MB pdf)

Slides: (6MB)

Each pixel in a photorealistic, computer generated picture is calculated by approximately integrating all the light arriving at the pixel, from the virtual scene. A common strategy to calculate these high-dimensional integrals is to average the estimates at stochastically sampled locations. The strategy with which the sampled locations are chosen is of utmost importance in deciding the quality of the approximation, and hence rendered image. We derive connections between the spectral properties of stochastic sampling patterns and the first and second order statistics of estimates of integration using the samples. Our equations provide insight into the assessment of stochastic sampling strategies for integration. We show that the amplitude of the expected Fourier spectrum of sampling patterns is a useful indicator of the bias when used in numerical integration. We deduce that estimator variance is directly dependent on the variance of the sampling spectrum over multiple realizations of the sampling pattern. We then analyse Gaussian jittered sampling, a simple variant of jittered sampling, that allows a smooth trade-off of bias for variance in uniform (regular grid) sampling. We verify our predictions using spectral measurement, quantitative integration experiments and qualitative comparisons of rendered images.

Fully-Connected CRFs with Non-Parametric Pairwise Potentials

Neill Campbell, Kartic Subr and Jan Kautz

To appear, CVPR, 2013

Preprint (pdf)

Supplementary material (pdf)

Conditional Random Fields (CRFs) are used for a diverse number of tasks, ranging from image denoising to object recognition. For images, they are commonly defined as a graph with nodes corresponding to individual pixels and pairwise links that connect pairs of nodes. Recent work has shown that fully-connected CRFs, where each node is connected to every other node, can be solved efficiently under the restriction that the pairwise term is a Gaussian kernel over a Euclidean feature space. In this paper, we generalize the pairwise terms to a non-linear dissimilarity measure that is not required to be a distance metric. To this end, we use an efficient embedding technique to estimate an approximate Euclidean feature space, in which the pairwise term can still be expressed as a Gaussian kernel. We demonstrate that the use of non-parametric models for the pairwise interactions, conditioned on the input data, greatly increases the expressive power whilst maintaining the efficient inference.

5D Covariance Tracing for Efficient Depth of Field and Motion Blur

Laurent Belcour, Cyril Soler, Kartic Subr, Nicolas Holzschuch and Fredo Durand

To appear, Transactions on Graphics, 2013

Preprint (1.2MB pdf)

2012 Tech report. (MIT-CSAIL-TR-2012-034) (pdf)

Slides: (8MB)

The rendering of effects such as motion blur and depth-of-field requires costly 5D integrals. We dramatically accelerate their computation through adaptive sampling and reconstruction based on the prediction of the anisotropy and bandwidth of the integrand. For this, we develop a new frequency analysis of the 5D temporal light-field, and show that first-order motion can be handled through simple changes of coordinates in 5D. We further introduce a compact representation of the spectrum using the covariance matrix and Gaussian approximations. We derive update equations for the $5 \times 5$ covariance matrices for each atomic light transport event, such as transport, occlusion, BRDF, texture, lens, and motion. The focus on atomic operations makes our work general, and removes the need for special-case formulas. We present a new rendering algorithm that computes 5D covariance matrices on the image plane by tracing paths through the scene, focusing on the single-bounce case. This allows us to reduce sampling rates when appropriate and perform reconstruction of images with complex depth-of-field and motion blur effects.

Accurate Binary Image Selection from Inaccurate User Input

Kartic Subr, Sylvain Paris, Cyril Soler, Jan Kautz

To appear,Computer Graphics Forum (Proc. of Eurographics 2013)

Source Code (4MB .zip): Noncommercial license

Slides: (10MB)

Preprint (pdf)

Selections are central to image editing, e.g., they are the starting point of common operations such as copy-pasting and local edits. Creating them by hand is particularly tedious and scribble-based techniques have been introduced to assist the process. By interpolating a few strokes specified by users, these methods generate precise selections. However, most of the algorithms assume a 100% accurate input, and even small inaccuracies in the scribbles often degrade the selection quality, which imposes an additional burden on users. In this paper, we propose a selection technique tolerant to input inaccuracies. We use a dense conditional random field (CRF) to robustly infer a selection from possibly inaccurate input. Further, we show that patch-based pixel similarity functions yield more precise selection than simple point-wise metrics. However, efficiently solving a dense CRF is only possible in low-dimensional Euclidean spaces, and the metrics that we use are high-dimensional and often non-Euclidean.We address this challenge by embedding pixels in a low-dimensional Euclidean space with a metric that approximates the desired similarity function. The results show that our approach performs better than previous techniques and that two options are sufficient to cover a variety of images depending on whether the objects are textured.

Interactive rendering of acquired materials on dynamic geometry using bandwidth prediction

Mahdi M. Bagher, Cyril Soler, Kartic Subr, Laurent Belcour, Nicolas Holzschuch

To appear, Trans on Viz and Comp Graphics (TVCG) 2013

Early version appeared at I3D 2012. Won best-paper-honarable-mention.

Journal paper (I3D) (pdf)

Conference paper (I3D) (pdf)

Video (on INRIA-HAL)

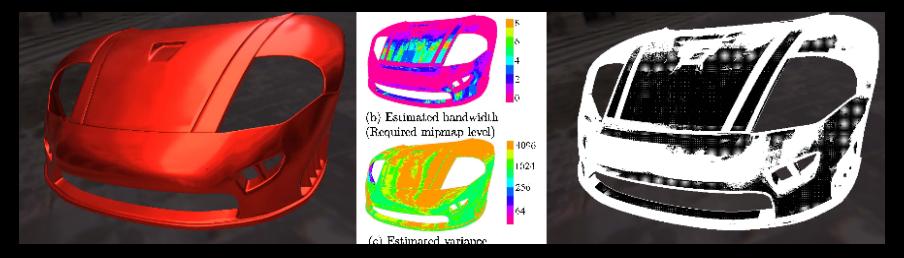
Shading complex materials such as acquired reflectances in multi-light environments is computationally expensive. Estimating the shading integral involves sampling the incident illumination independently at several pixels. The number of samples required for this integration varies across the image, depending on an intricate combination of several factors. Adaptively distributing computational budget across the pixels for shading is therefore a challenging problem. In this paper we depict complex materials such as acquired reflectances, interactively, without any precomputation based on geometry. We first estimate the approximate spatial and angular variation in the local light field arriving at each pixel. This \emph{local bandwidth} accounts for combinations of a variety of factors: the reflectance of the object projecting to the pixel, the nature of the illumination, the local geometry and the camera position relative to the geometry and lighting. We then exploit this bandwidth information to adaptively sample for reconstruction and integration. For example, fewer pixels per area are shaded for pixels projecting onto diffuse objects, and fewer samples are used for integrating illumination incident on specular objects.

Real-time Rough Refraction

Charles De Rousiers, Adrien Bousseau, Kartic Subr, Nicolas Holzschuch, Ravi Ramamoorthi

TVCG Jan 2012 (invited paper)

Best Paper at I3D 2011

Preprint (pdf)

Video (on YouTube)

We present an algorithm to render objects of transparent materials with rough surfaces in real-time, under distant illumination. Rough surfaces cause wide scattering as light enters and exits objects, which significantly complicates the rendering of such materials. We present two contributions to approximate the successive scattering events at interfaces, due to rough refraction : First, an approximation of the Bidirectional Transmittance Distribution Function (BTDF), using spherical Gaussians, suitable for real-time estimation of environment lighting using pre-convolution; second, a combination of cone tracing and macro-geometry filtering to efficiently integrate the scattered rays at the exiting interface of the object. We demonstrate the quality of our approximation by comparison against stochastic raytracing.

Real-time Rendering of Heterogeneous Translucent Objects with Arbitrary Shapes

Yajun Wang, Jiaping Wang, Nicolas Holzschuch, Kartic Subr, Baining Guo

To appear, Computer Graphics forum 2010, (Proceedings of Eurographics 2010)

Preprint (pdf)

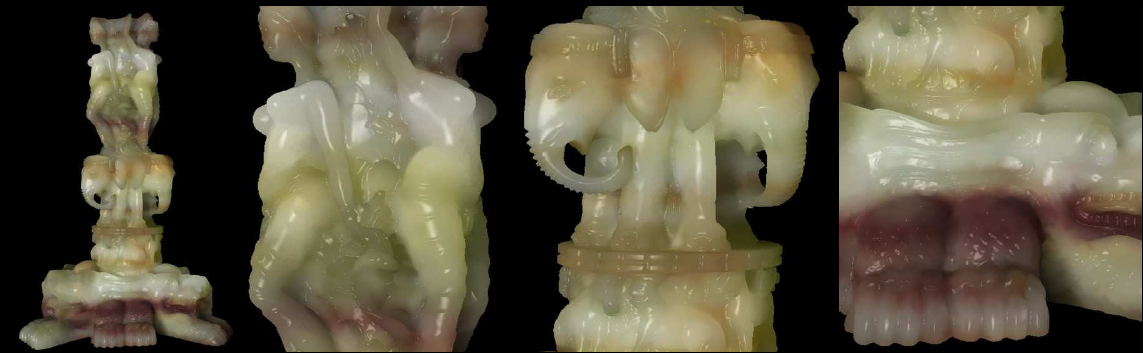
In this paper, we present a real-time algorithm for rendering translucent objects of arbitrary shapes. We approxi mate the light scattering process inside the object with the diffusion equation, which we solve on-the-fly using the GPU. Our algorithm is general enough to handle arbitrary geometry, heterogeneous materials, deformable objects and modifications of lighting, all in real-time. Our algorithm works as follows: in a pre-processing step, we discretize the object into a regular 4-connected structure (QuadGraph). Thanks to its regular connectivity, this structure is easily packed into a texture and stored on the GPU. At runtime, we use the QuadGraph stored on the GPU to solve the diffusion equation, in real-time, taking into account the varying input conditions: the incoming light and the object material and geometry. We handle deformable objects, as long as the deformation does not change the topological structure of the objects.

Edge-preserving Multiscale Image Decompostion based on Local Extrema

Kartic Subr, Cyril Soler, Fredo Durand

To appear, Transactions on Graphics 2009 (SIGGRAPH Asia)

Preprint (pdf) . . . . . . . . . Supplementary material (pdf)

Video (.mov ~46 MB) . . . Unverified source code - here (Courtesy Drake Guan)

Slides (ppt)

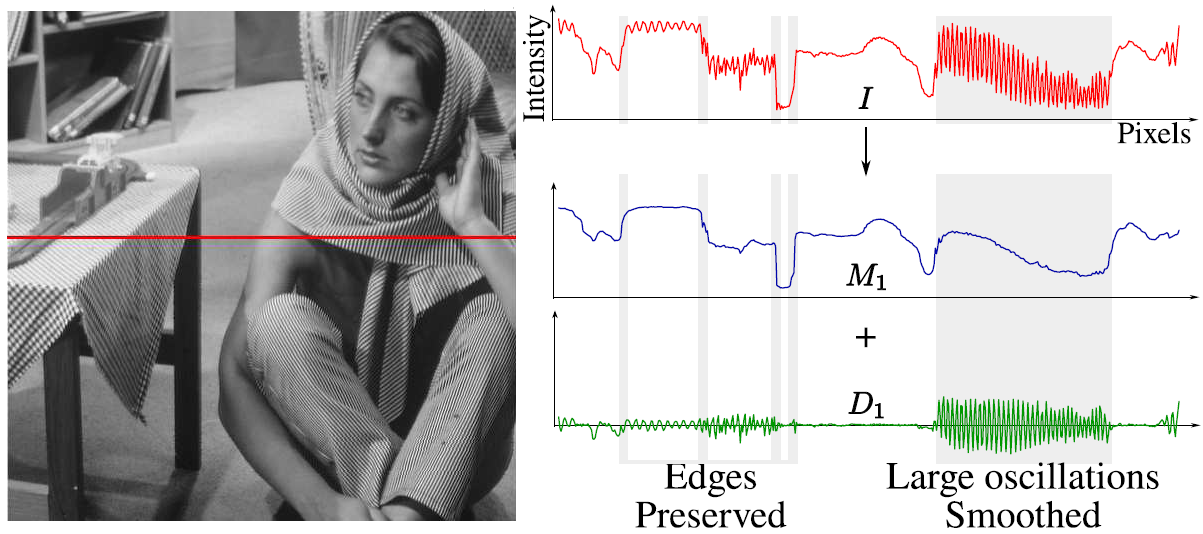
We propose a new model for detail that inherently captures oscillations, a key property that distinguishes textures from individual edges. Inspired by techniques in empirical data analysis and morphological image analysis, we use the local extrema of the input image to extract information about oscillations: We define detail as oscillations between local minima and maxima. Building on the key observation that the spatial scale of oscillations are characterized by the density of local extrema, we develop an algorithm for decomposing images into multiple scales of superposed oscillations. Current edge-preserving image decompositions assume image detail to be low contrast variation. Consequently they apply filters that extract features with increasing contrast as successive layers of detail. As a result, they are unable to distinguish between high-contrast, fine-scale features and edges of similar contrast that are to be preserved.We compare our results with existing edge-preserving image decomposition algorithms and demonstrate exciting applications that are made possible by our new notion of detail.

Fourier Depth of Field

Cyril Soler, Kartic Subr, Fredo Durand, Nicolas Holzschuch, Francois Sillion

ACM Transactions on Graphics, 2009

Paper (pdf)

Slides (ppt)

Optical systems used in photography and cinema produce depth of field effects, that is, variations of focus with depth. These effectsFG can be simulated in image synthesis by integrating incoming radiance at each pixel over a finite aperture: Aperture integration can be extremely costly for defocused areas with high variance in the incoming radiance, since many samples are required in a Monte Carlo integration. However, using many aperture samples is wasteful in focused areas where the integrand varies very little. Similarly, image sampling in defocused areas should be adapted to the very smooth appearance variations due to blurring. This paper introduces an analysis of focusing and depth of field in the frequency domain, allowing a practical characterization of a light field's frequency content both for image and aperture sampling. Based on this analysis we propose an adaptive depth of field rendering algorithm which optimizes sampling in two important ways. First, image sampling is based on conservative bandwidth prediction and a splatting reconstruction technique ensures correct image reconstruction. Second, at each pixel the variance in the radiance over the aperture is estimated, and used to govern sampling. This technique is easily integrated in any sampling-based renderer, and vastly improves performance.

Sampling Strategies for Efficient Monte Carlo Image Synthesis

Kartic Subr

Ph.D. Dissertation, May 2008

Adivsor: James Arvo

Full dissertation (pdf)

Introduction only (pdf)

Slides (pdf)

The gargantuan computational problem of light transport in physically based image synthesis is popularly made tractable by reduction to a series of sampling problems. This reduction is a consequence of using Monte Carlo integration at various stages of the transport process. In this document we describe analytic and computational tools for efficient sampling, and apply them at three stages of the light transport process: Sampling the image, sampling the camera aperture and sampling direct illumination due to distant light sources. We also adapt a standard statistical technique of inductive inference to assess different Monte Carlo sampling strategies that solve the light transport problem.

Statistical Hypothesis Testing for Assessing Monte Carlo Estimators: Applications to Image Synthesis

Kartic Subr, James Arvo

ACM Pacific Graphics, 2007

Paper (pdf)

Slides (pdf)

Image synthesis algorithms are commonly compared on the basis of running times and/or perceived quality of the generated images. In the case of Monte Carlo techniques, assessment often entails a qualitative impression of conver- gence toward a reference standard and severity of visible noise; these amount to subjective assessments of the mean and variance of the estimators, respectively. In this paper we argue that such assessments should be augmented by well-known statistical hypothesis testing methods. In par- ticular, we show how to perform a number of such tests to assess random variables that commonly arise in image syn- thesis such as those estimating irradiance, radiance, pixel color, etc. We explore five broad categories of tests: 1) de- termining whether the mean is equal to a reference stan- dard, such as an analytical value, 2) determining that the variance is bounded by a given constant, 3) comparing the means of two different random variables, 4) comparing the variances of two different random variables, and 5) verify- ing that two random variables stem from the same parent distribution. The level of significance of these tests can be controlled by a parameter. We demonstrate that these tests can be used for objective evaluation of Monte Carlo estima- tors to support claims of zero or small bias and to provide quantitative assessments of variance reduction techniques. We also show how these tests can be used to detect errors in sampling or in computing the density of an importance function in MC integrations.

Steerable Importance Sampling

Kartic Subr, James Arvo

IEEE Conference on Interactive Raytracing, 2007

Paper (pdf)

Slides (pdf)

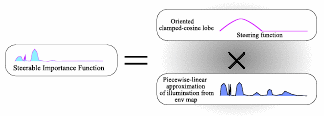
We present an algorithm for efficient stratified importance sampling of environment maps that generates samples in the positive hemi- sphere defined by local orientation of arbitrary surfaces while ac- counting for cosine weighting. The importance function is dynam- ically adjusted according to the surface normal using steerable ba- sis functions. The algorithm is easy to implement and requires no user-defined parameters. As a preprocessing step, we approximate the incident illumination from an environment map as a continuous piecewise linear function on S^2 and represent this as a triangu- lated height field. The product of this approximation and a dynami- cally orientable steering function, viz. the cosine lobe, serves as an importance sampling function. Our method allows the importance function to be sampled with an asymptotic cost of O(logn) per sam- ple where n is the number of triangles. The most novel aspect of the algorithm is its ability to dynamically compute normalization fac- tors which are integrals of the illumination over the positive hemi- spheres defined by the local surface normals during shading. The key to this feature is that the weight variation of each triangle due to the clamped cosine steering function can be well approximated by a small number of spherical harmonic coefficients which can be ac- cumulated over any collection of triangles, in any orientation, with- out introducing higher-order terms. Consequently, the weighted in- tegral of the entire steerable piecewise-linear approximation is no more costly to compute than that of a single triangle, which makes re-weighting and re-normalizing with respect to any surface ori- entation a trivial constant-time operation. The choice of spherical harmonics as the set of basis functions for our steerable importance function allows for easy rotation between coordinate systems. An- other novel element of our algorithm is an analytic parametrization for generating stratified samples with linearly-varying density over a triangular support.

Greedy Algorithm for Local Contrast Enhancement of Images

Kartic Subr, Aditi Majumder, Sandy Irani

ICIAP 2005

pdf

We present a technique that achieves local contrast enhance- ment by representing it as an optimization problem. For this, we first introduce a scalar objective function that estimates the average local contrast of the image; to achieve the contrast enhancement, we seek to maximize this objective function subject to strict constraints on the lo- cal gradients and the color range of the image. The former constraint controls the amount of contrast enhancement achieved while the latter prevents over or under saturation of the colors as a result of the en- hancement. We propose a greedy iterative algorithm, controlled by a single parameter, to solve this optimization problem. Thus, our contrast enhancement is achieved without explicitly segmenting the image either in the spatial (multi-scale) or frequency (multi-resolution) domain. We demonstrate our method on both gray and color images and compare it with other existing global and local contrast enhancement techniques.

Order Independent, Attenuation-Leakage Free Splatting using FreeVoxels

Kartic Subr, Pablo Diaz-Gutierrez, Renato Pajarola, M. Gopi

Technical Report ifi-2007.01, Department of Informatics, Unviersity of Zurich

pdf

In splatting-based volume rendering, there is a well-known problem of attenuation leakage, that occurs due to blend- ing operations on adjacent voxels. Hardware accelerated volume splatting exploits the graphics hardware’s alpha- blending capability to achieve attenuation from layers of voxels. However, this alpha-blending functionality results in accumulated errors(attenuation leakage), if performed on multiple overlapping alpha-values. In this paper, we in- troduce the concept of FreeVoxels which are self-sufficient structures in which the data required for operations on voxels are pre-computed and stored. These data are used to render each voxel independently in any order and also to eliminate the attenuation leakage. The drawback of the FreeVoxel data structure, that this paper does not address, is that it requires a significant amount of extra storage. De- spite that, the advantages of a FreeVoxel data structure war- rant extensive investigations in this direction. Specifically, FreeVoxel can be used, other than in solving the attenu- ation leakage problem, to achieve order-independent ren- dering; in parallel volume rendering, use of FreeVoxels al- lows arbitrary static data distribution with no data migra- tion; it also enables synchronization-free rendering with- out compromising load-balancing. A similar data structure with comparable memory requirements has also been used for opacity based occlusion culling in volume rendering by [10]. In this paper, we also describe a hierarchical exten- sion of FreeVoxels that lends itself to multi-resolution ren- dering.